Research
Mathematical frameworks for machine learning; LiDAR/3D point clouds; numerical analysis, PDEs, and functional analysis
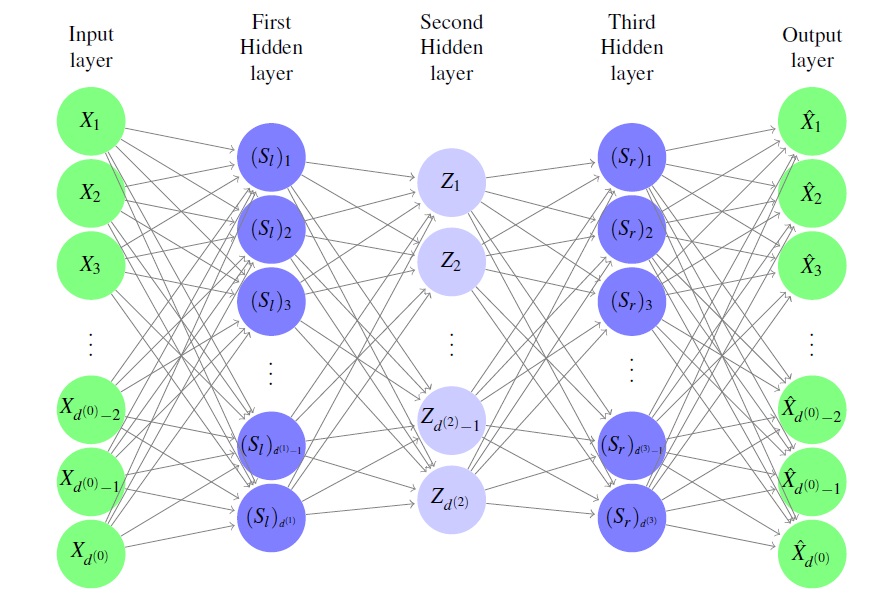
My research develops mathematically grounded tools for modern data problems, with a focus on building mathematical frameworks for machine learning. A recurring theme is designing representations and features that are both computationally effective and mathematically interpretable. This includes feature engineering inspired by measure theory and functional analysis, and dimensionality reduction methods (e.g., PCA and autoencoders) for high-dimensional and geometric data such as LiDAR/3D point clouds.
I also work in numerical analysis and partial differential equations (PDEs), including PDE-based models for physical phenomena in porous media and geoscience applications (e.g., methane hydrates and adsorption models).
Before focusing on machine learning and computational research, I worked in functional analysis, with particular emphasis on Banach space theory and Orlicz spaces. This early work played a central role in my decision to pursue a Ph.D. in mathematics. My broad background continues to shape how I approach research: I enjoy connecting ideas across areas—from pure mathematics to computation and real-world data.
Machine learning on LiDAR / 3D point clouds
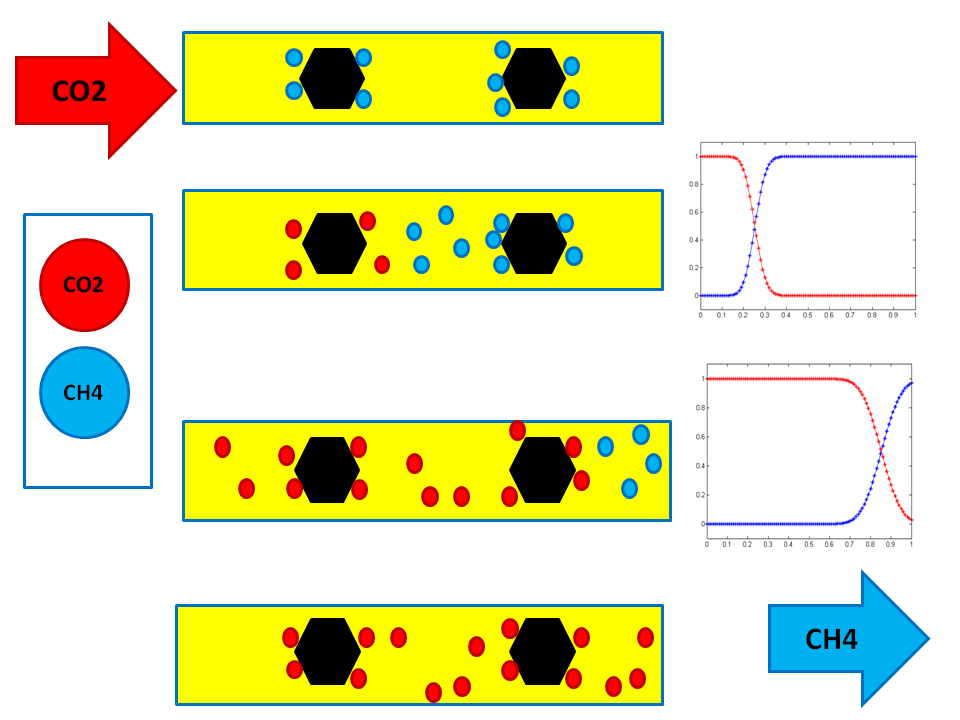
My work on LiDAR data grew out of research collaborations in data science and geometry-informed learning. A major motivation is that point cloud data are high-dimensional, noisy, and often contain structure at multiple scales. I am interested in improving classification pipelines by combining: (i) mathematically motivated feature engineering, (ii) dimensionality reduction, and (iii) learning models suited to geometric data.One line of work focuses on using learned representations (e.g., autoencoders) together with engineered features to classify points into relevant classes (for example, distinguishing ground versus non-ground points and refining labels based on morphology and local structure). Typical features in LiDAR datasets include spatial coordinates, intensity, number of returns, and (when available) RGB information. Beyond standard feature sets, my goal is to develop descriptors motivated by rigorous mathematical ideas (e.g., measure-theoretic quantities defined on dyadic neighborhood structures) to improve performance and interpretability.
Remote sensing: vegetation classification and climate-related applications
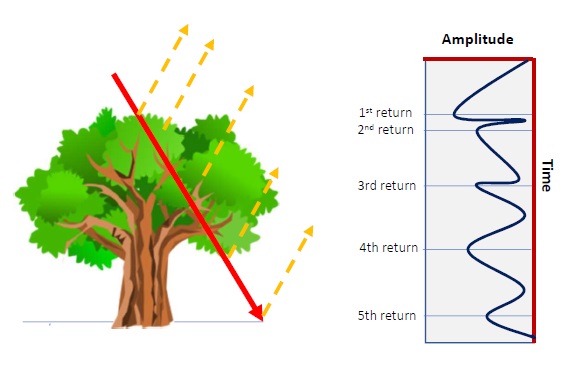
Over the last decade, collaborators in remote sensing and geospatial analysis have collected and analyzed LiDAR point cloud data across different sites using both direct (labor-intensive) and indirect methods. A motivating application is estimating forest structure parameters from LiDAR, including leaf area index (LAI) and related canopy measures. A general approach is to combine engineered features and multi-scale geometric descriptors with dimensionality reduction (linear methods such as PCA and nonlinear methods such as autoencoders), followed by learning models such as feed-forward neural networks or ensemble methods. Automating classification and structural estimation can significantly accelerate analysis pipelines for large-scale forest data.

Methane hydrates
I have studied mathematical models for the evolution of methane hydrates in hydrate zones, including simplified models that incorporate parameter-dependent solubility constraints. These constraints can be represented using nonlinear complementarity conditions. This work includes analysis of solvability and properties of fully discrete numerical schemes.